list
contents
related file
- cpython/Objects/listobject.c
- cpython/Objects/clinic/listobject.c.h
- cpython/Include/listobject.h
memory layout
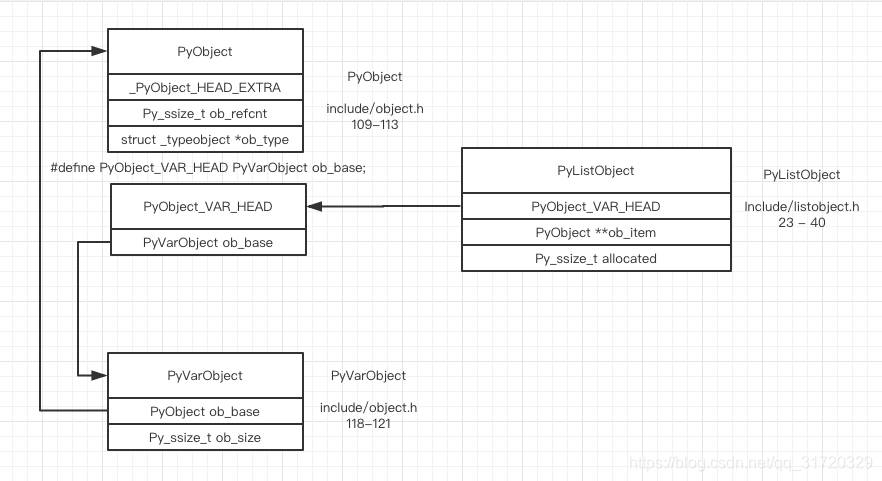
append
the basic object’s name is list, but the actual implementation is more like a vector in C++
let’s initialize an empty list
l = list()
field ob_size stores the actual size, it’s type is Py_ssize_t which is usually 64 bit, 1 << 64 can represent a very large size, usually you will run out of RAM before overflow the ob_size field

and append some elements into the list
l.append("a")
ob_size becomes 1, and ob_item will point to a newly malloced block with size 4

l.append("b")
l.append("c")
l.append("d")
now the list is full

if we append one more element
l.append("e")
this is the resize pattern
/* cpython/Objects/listobject.c */
/* The growth pattern is: 0, 4, 8, 16, 25, 35, 46, 58, 72, 88, ... */
/* currently: new_allocated = 5 + (5 >> 3) + 3 = 8 */
new_allocated = (size_t)newsize + (newsize >> 3) + (newsize < 9 ? 3 : 6);

you can see that it’s actually more like a C++ vector
pop
the append operation will only trigger the list’s resize when the list is full
what about pop ?
>>> l.pop()
'e'

>>> l.pop()
'd'
the realloc is called and the malloced size is shrinked, actually the resize function will be called each time you call pop
but the actual realloc will be called only if the newsize falls lower than half the allocated size
/* cpython/Objects/listobject.c */
/* allocated: 8, newsize: 3, 8 >= 3 && (3 >= 4?), no */
if (allocated >= newsize && newsize >= (allocated >> 1)) {
/* Do not realloc if the newsize deos not fall
lower than half the allocated size */
assert(self->ob_item != NULL || newsize == 0);
/* only change the ob_size field */
Py_SIZE(self) = newsize;
return 0;
}
/* ... */
/* 3 + (3 >> 3) + 3 = 6 */
new_allocated = (size_t)newsize + (newsize >> 3) + (newsize < 9 ? 3 : 6);

sort
timsort
the algorithm CPython used in sorting list is timsort, it’s quiet complicated
>>> l = [5, 9, 17, 11, 10, 14, 2, 8, 12, 19, 4, 13, 3, 0, 16, 1, 6, 15, 18, 7]
>>> l.sort()
I’ve modified some parameter in source code for illustration, I will explain later
a structure named MergeState is created for helping the timsort algorithm

this is the state after preparing

assume minrun is 5, we will see what minrun is and how minrun calculated later, for now, we run the sort algorithm and ignore these details for illustration

binary_sort will be used for sorting a group of elements, the number of elements in a group is called run(minrun) here
after binary_sort the first group, nremaining becomes 15, count_run becomes 2, n of the MergeState becomes 1, because the pending is preallocated, the elements in pending is meaningless, n means how many elements in the pending array does mean something

after binary_sort the second group

the second group is sorted by binary_sort, and the next index of pending stores the information of the second group
we can learn from the above graph that pending act as a stack, every time a group is sorted, the group info will be pushed onto this stack, a function named merge_collapse will be called after the psuh operation
/* cpython/Objects/listobject.c */
/* Examine the stack of runs waiting to be merged, merging adjacent runs
* until the stack invariants are re-established:
*
* 1. len[-3] > len[-2] + len[-1]
* 2. len[-2] > len[-1]
*/
static int
merge_collapse(MergeState *ms)
{
struct s_slice *p = ms->pending;
assert(ms);
while (ms->n > 1) {
Py_ssize_t n = ms->n - 2;
if ((n > 0 && p[n-1].len <= p[n].len + p[n+1].len) ||
/* case 1:
pending[0]: [---------------------------]
pending[1]: [-----------------------] (n)
pending[2]: [-----------------------]
... (ms->n)
len(pending[0]) <= len(pending[1]) + len(pending[2])
*/
(n > 1 && p[n-2].len <= p[n-1].len + p[n].len)) {
/* case 2:
...
pending[3]: [-----------------------------------------------------------------]
pending[4]: [-----------------------------------------------------------------]
pending[5]: [-----------------------] (n)
pending[6]: [-----------------------]
pending[7]: [-----------------------] (ms->n)
len(pending[3]) <= len(pending[4]) + len(pending[5])
*/
if (p[n-1].len < p[n+1].len)
/* pending[0]: [-----------------] (new_n)
pending[1]: [-----------------------] (n)
pending[2]: [-----------------------]
*/
--n;
if (merge_at(ms, n) < 0)
return -1;
}
else if (p[n].len <= p[n+1].len) {
/* case 3:
pending[0]: [--------------] (n)
pending[1]: [--------------]
*/
if (merge_at(ms, n) < 0)
return -1;
}
else
break;
}
return 0;
}
the current state is case 3, merge_at will merge the two runs at stack indices i and i+1
merge_at
merge_at is the combination of merge_sort and galloping mode

after merge_collapse, the first two runs are merged and valid length of pending becomes 1

after binary_sort the next run

the merge_collapse won’t merge any of the run because the stack invariants are good
after binary_sort the final run

it meets case 1, and the last two run will be merged first

in the while loop of merge_collapse, merge will happen again in case 3, after this merge, we’ve finished our timsort algorithm and all the ob_item in list are sorted

galloping mode
if we are merging these two arrays

we can use binary search to find the the max element that is smaller than the first element in the right, and copy these elements together instead of merging one by one

we can also do that from right to left

read more detail in listsort.txt
binary_sort
before delegating the call to binary_sort, a function named count_run will be called first to calculate the longest increasing or descending subarray begin at index 0

so that binary_sort can sort the range begin at index 2, and end at index 4
the subarray before start is sorted, and we need to sort all the rest elements from start to the end

first we set a variable pivot’s value to start’s value, perform binary search in the left subarray to find the first element that is greater than pivot
do {
p = l + ((r - l) >> 1);
IFLT(pivot, *p)
r = p;
else
l = p+1;
} while (l < r);
then we move every element from l to start forawrd, and set element in start to pivot

we perform binary search again, this time element in index 2 is selected, we move every element from the selected index to start forward again

and set the value in selected element’s index to pivot

we need to perform the final binary search

the selected element is in index 2, after move every element from l to start forawrd

and set element in start to pivot, we’ve finished the binary_sort algorithm

run
actually minrun will be computed in the following function, if the current run number is lower than 64, it will be binary_sort directly, else half of it’s size will be shrink until there’s a result size lower than 64
I’ve changed this constant to a smaller value so that the example above can fit into my graph
static Py_ssize_t
merge_compute_minrun(Py_ssize_t n)
{
Py_ssize_t r = 0; /* becomes 1 if any 1 bits are shifted off */
assert(n >= 0);
while (n >= 64) {
r |= n & 1;
n >>= 1;
}
return n + r;
}
time complexity
time complexity of timsort

free_list
#ifndef PyList_MAXFREELIST
#define PyList_MAXFREELIST 80
#endif
static PyListObject *free_list[PyList_MAXFREELIST];
static int numfree = 0;
there exists per process global variable named free_list

if we create a new list object, the memory request is delegate to CPython’s memory management system
a = list()

del a
the destructor of the list type will stores the current list to free_list (if free_list is not full)

next time you create a new list object, free_list will be checked if there is available objects you can use directly, if so, allocate from free_list, if not, allocate from CPython’s memory management system
b = list()

by caching list objects in free_list can
- improve performance
- reduce memory fragmentation